Scaling

Introduction

Before you submit large production runs on a bwHPC cluster you should define an optimal number of resources required for your compute job. Poor job efficiency means that hardware resources are wasted and a similar overall result could have been achieved using fewer hardware resources, leaving those for other jobs and reducing the queue wait time for all users.

The main advantage of today‘s compute clusters is that they are able to perform calculations in parallel. If and how your code is able to be parallelized is of fundamental importance for achieving good job efficiency and performance on an HPC cluster. A scaling analysis is done by identifying the number of resources (such as the number of cores, nodes, or GPUs) that enable the best performance for a given compute job.

Reasons for poor job efficiency

Some simple causes for poor overall job efficiency are:

• Poor choice of resources compared to the size of the nodes leaves part of the node blocked, but doing nothing:
  • Multiple of --ntasks-per-node is not the number of cores on a node (e.g. 48)
  • Too much (un-needed) memory or disk space requested
• More cores requested than are actually used by the job
• More cores used for a single mpi/openmp parallel computation than useful
• Many small jobs with a short runtime (seconds in extreme cases)
• One-core jobs with very different run-times (because of single-user policy)

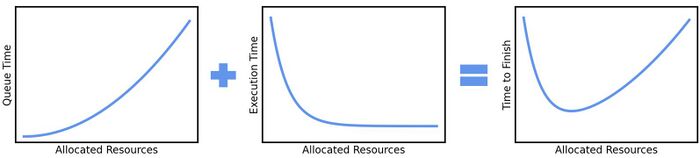
Time to Finish: Considering Resources vs. Queue Time

When a job is submitted to the Slurm scheduler, the job first waits in the queue before being executed on the compute nodes. The amount of time spent in the queue is called the queue time. The amount of time it takes for the job to run on the compute nodes is called the execution time.

The figure below shows that the queue time increases with increasing resources (e.g., CPU cores) while the execution time decreases with increasing resources. One should try to find the optimal set of resources that minimizes the "time to solution" which is the sum of the queue and execution times. A simple rule is to choose the smallest set of resources that gives a reasonable speed-up over the baseline case.

Scalability

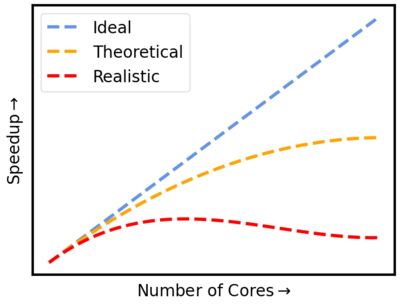
When you run a parallel program, the problem has to be cut into several independent pieces. For some problems, this is easier than for others - but in every case, this produces an overhead of time used to divide the problem, distribute parts of it to tasks, and stitch the results together. For a theoretical amount of "infinite calculations", calculating each problem on one single core would be the most efficient way to use the hardware In extreme cases, when the problem is very hard to divide, using more compute cores, can even make the job finish later.

For real calculations, it is often impractical to wait for calculations to finish if they are done on a single core. Typical calculation times for a job should stay under 2 days, or up to 2 weeks for jobs that cannot use more cores efficiently. Any longer and the risks such as node failures, cluster downtimes due to maintenance, and getting (possibly wrong) results after too much wait time can become too much of a problem.

A common way to assess the efficiency of a parallel program is through its speedup. Here, speedup is defined as the ratio of the time a serial program needs to run to the time for the parallel program that accomplishes the same work.

Speedup= Time(serial program) / Time(parallel program)

A simple example would be a calculation that takes 1000 hours on 1 core. Without any overhead from parallelization, the same calculation run on 1000 cores would need 1000/100= 10 hours, the ideal speedup. More realistically, such a calculation for parallelized code would need around 30 hours.

However, there is a theoretical upper limit on how much faster you can solve the original problem by using additional cores (Amdahl's Law ((Amdahl's Law)). While a considerable part of a compute job might parallelize nicely, there is always some portion of time spent on I/O, such as saving or reading from disc, network limitations, communication overhead, or performing calculations that cannot be parallelized, thus reducing the speedup that I possible by simply adding more computational resources.

From the speedup, a useful definition of efficiency can be derived:

Efficiency = Speedup / Number of cores = Time(serial program) / (Time(parallel program) * Number of cores)

The efficiency allows for an estimation of how well your code is using additional cores, and how much of the resources are lost by doing parallelization overhead calculations. Coming back to the previous example, we can now use the time of a serial calculation (1000 hours), the time our parallelized code took to finish (30 hours), the number of cores we used (100 cores), and calculate the efficiency.

Efficiency = 1000 / (30 * 100)=0.3

This shows that for this example, only 30% of the resources are used to solve the problem, while 70% of our resources are spent on parallelization overhead. A semi-arbitrary cut-off for determining if a job is well-scaled is if they waste 50% of the computation or less on parallelization overhead.

In many cases, the time needed for calculating a given code in serial, on a single core, is not accessible, as this would take a very long time and is usually the reason why an HPC cluster is needed in the first place. To circumvent this, the relative speedup when doubling the number of cores is calculated.

Relative Speedup (16->32) = Time(16 Cores) / Time(32 Cores)

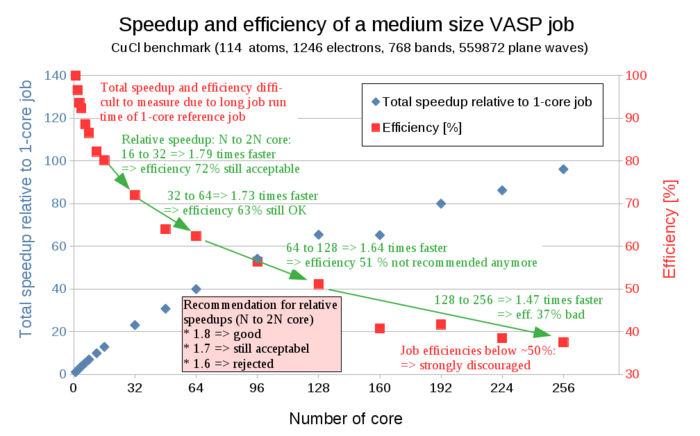
The relative speedup obtained by doubling the number of cores can be used as a rough guideline for a scaling analysis. If doubling the number of cores results in a relative speedup of above 1.8, the scaling is considered good. Above 1.7 is considered acceptable, while a relative speedup of less than 1.7 should usually be avoided. Overall, this leads us to the following rules of thumb or recipe for determining the number of cores to use:

(1) Optimizing resource usage is most relevant when you submit many jobs or resource-heavy jobs. For smaller projects, simply try to use a reasonable core number and you are done.

(2) If you plan to submit many jobs, verify that the core number is acceptable. If the jobs use N cores (i.e. N is 96 for a two-node job), then run the same job with N/2 cores (in this example 48 cores).

(3) To calculate the speedup, you then divide the (longer) run time of the N/2-core-job by the (shorter) run time of the N-core-job. Typically the speedup is a number between 1.0 (no speedup at all) and 2.0 (perfect speedup - all additional cores speed up the job).

(4a) IF the speedup is better than a factor of 1.7, THEN using N cores is perfectly fine.

(4b) IF the speedup is worse than a factor of 1.7, THEN using N cores wastes too many resources and N/2 cores should be used.

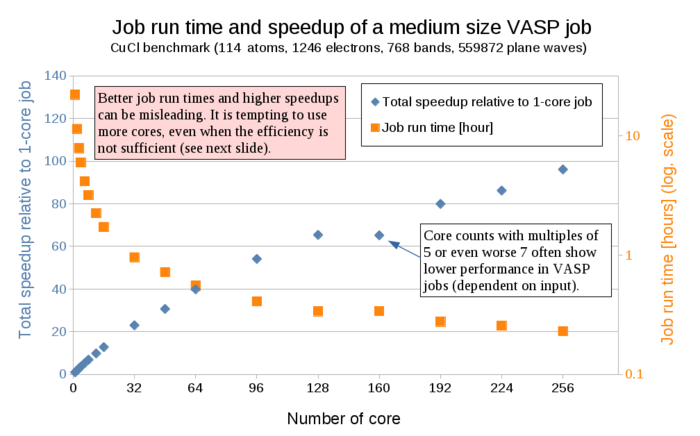
You can see data from a real example using the program VASP in the following